第1章 SAT的历史

前言：可满足性的概念

可满足性源于逻辑学

逻辑：有效性(Validity)和一致性(Consistency)。

使用否定()来联系两者：从到的论证是有效的当且仅当是不一致的。

有效性和一致性是看待同一事物的两种方式，都可以通过句法(Syntax)和语义(Semantics)来表达。

句法

句法产生了证明论(Proof Theory)，针对公理系统的推导。（欧氏几何）

• 有效性：可推导性(Derivability)：由句法定义​
• 一致性：是一致的，当且仅当，无法推导出矛盾​

语义

语义产生了模型论(Model Theory)，主要研究句子和“世界”的关系。

• 真理：“与世界相对应”
• 代数结构：​，D代表世界W中非空对象的集合，R代表一种映射（解释）
• 句子p在W中为真：句子p的解释在世界W中符合。
• 句子p在A中为真：
• 有效性：从到的论证是有效的（记作），当且仅当，对于所有代数结构A，若，则成立。
• 一致性：可满足性(Satisfiability)：是可满足的，当且仅当，存在代数结构A，使得​成立。

在完备的公理系统中，句法和语义是一致的。

亚里士多德和三段论（公元前4世纪）

主语(S)+谓语(P)+四种命题：“与世界相对应”

• 普遍肯定(A)：所有S是P为真
• 普遍否定(E)：没有S是P为真
• 特殊肯定(I)：一些S是P为真
• 特殊否定(O)：一些S不是P为真​

古典时期假设：逻辑是双值的，不能包含空集

• A和E不能同时为真，I和O不能同时为假

三段论

三段论：形如且是A，E，I，O命题

如何反驳？以现实为例

三段论推理

将转化为三段论​

• 公理1：

• 公理2：

• 规则1：推出

• 规则2：推出

• 规则3：没有X是Y推出没有Y是X

• 规则4：推出

• 公理2：
• 规则3：​
• 规则4：

斯多葛(Stoics)学派（公元前3世纪）

• 使用符号表达命题
• 命题推理规则：
  • 前提推理(Modus Ponens)：
  • 否定推理(Modus Tollens)：
  • 选言推理(Disjunctive Syllogism)：​
  • 假设推理(Hypothetical Syllogism)：​

过渡时期

中世纪：

• 更复杂的语法
• 集合论的雏形
• 使用图形理解逻辑

文艺复兴：莱布尼兹，引入“部分”符号，“实加法”符号和“恒等式”符号

• 幂等律：
• 交换律：
• 结合律：
• 部分：当且仅当

乔治布尔和布尔代数（19世纪）

布尔代数：

• 是二元运算符，是一元运算符，B是封闭的，​

• 集合运算符：补集：，并集：，交集：

韦恩(Venn)图：一种与布尔代数完美同构的图解方法。

三段论、布尔代数、集合

V代表x和y相交形成的非空子集。

弗雷德和罗素悖论

弗雷德在《算数原理》中提出：可以使用由五个基本逻辑定律、几个量词定律和几个函数公理组成的“逻辑公理”推导出集合论，数论，分析中的所有定理。

罗素悖论：

罗素与怀特海德在《数学原理》中提出类型理论：规定对象只能与相同或更高类型的对象进行关联，避免了集合的自我包含。

哥德尔不完备定理

逻辑主义（弗雷德、罗素、希尔伯特）：数学可以从有限的公理中推导出来（完备）

哥德尔不完备定理：能够制定算数定律的公理系统一定是不完备的

• 自指悖论（罗素悖论，哥德尔不完备定理，停机问题）

• 一阶逻辑的完备性

香农和逻辑电路

布尔函数的展开：

简化操作：

• ​

解析和DPLL算法

前提：

• 一阶逻辑具有完备性
• 逻辑电路-计算机

希望自动证明一阶逻辑中的定理

• Davis-Putman Procedure
• Loveland和Logemann对DPP进行改进：DPLL
  • 赋值操作
• Tseitin扩展解析：将复杂公式化简

解析的复杂性

• 树解析：从现有子句推出新子句
• 序列解析：从一个子句推出新子句

树解析效率低下，存在冗余

基于DPLL框架的SAT求解器存在类似的低效率和冗余

基于解析的SAT求解器改进

变量选择/赋值选择：

• 最短子句
• 选择正负文字差异最大的变量
• 贪婪启发
• 满足更多的子句（可满足友好）
• 正负值搜索空间大小类似（不可满足友好）
• 变量赋值活动（VSIDS）

前瞻（Lookahead）：同时尝试几个变量的赋值，选择最优的继续

深度优先前瞻：重启

子句学习

特殊SAT问题

• 2-SAT
• Horn：每个子句最多含有一个正文字
  • ​代表或​
• 线性规划相关：CNF可以转化为矩阵—整数规划—放宽为线性规划问题
• SLUR：包含Horn，Renameable Horn，Extended Horn，CC-balanced等结构的算法：可以在多项式时间内判断SAT问题是否符合其中包含的类

• q-Horn：通过列乘-1，行和列重新排列

  • 东北象限：全为0
  • 西北象限：Horn表达式
  • 东南象限：2-SAT表达式
  • 西南象限：没有正文字

• 匹配：二分图，存在完全匹配

• k-BRLR：每个变量的正负文字出现总和不超过k次

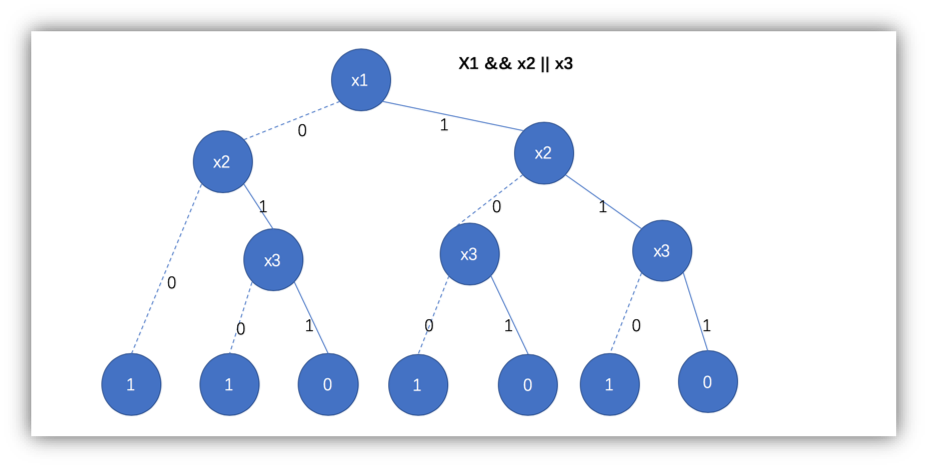
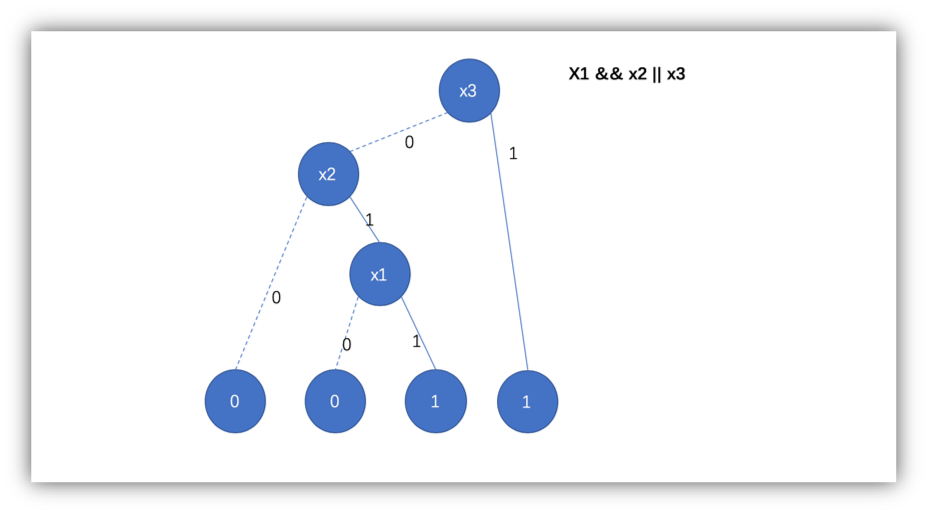
随机局部搜索(Stochastic Local Search)

SLS是解决困难组合问题最成功和最广泛使用的通用策略之一

• 模拟退火
• 进化算法

应用于SAT问题的SLS算法：

• GSAT算法（90年代比DPLL更快）
  • 遗传算法（适应度评估—选择—交叉—变异）
• GSAT+子句权重
• GSAT+随机游走
• SAPS算法：基于子问题分割求解
• DDFW算法：变量之间的动态依赖

MAX-SAT

MAX-SAT：满足最多的子句数量

• 分支定界法
• 转化为SAT问题

MAX-2-SAT：每个子句最多两个文字

总结

没讲的部分：

• 基于概率的SAT分析（1.21，1.22）
• 非线性公式（1.25）
• 伪布尔形式（1.26）
• 量化布尔公式（1.27）