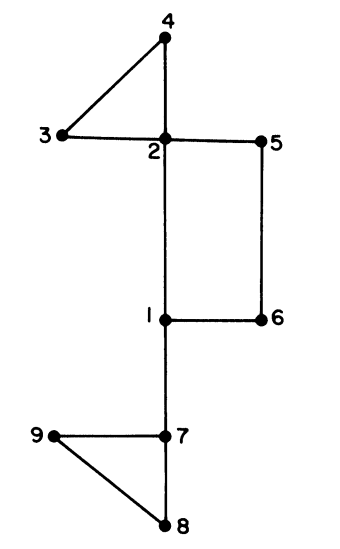
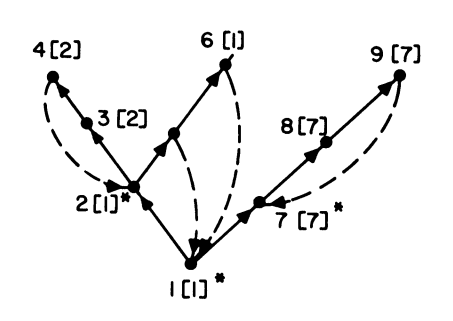
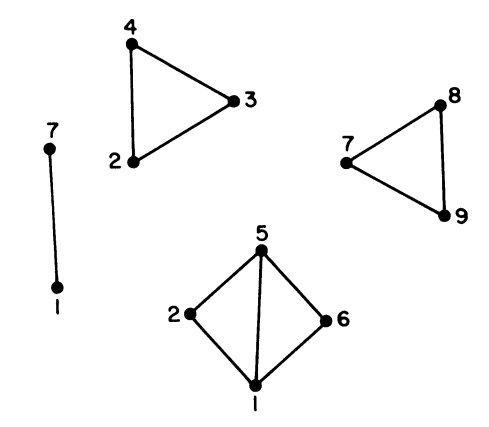
研究动机(重新审视HT串行算法)
文章贡献
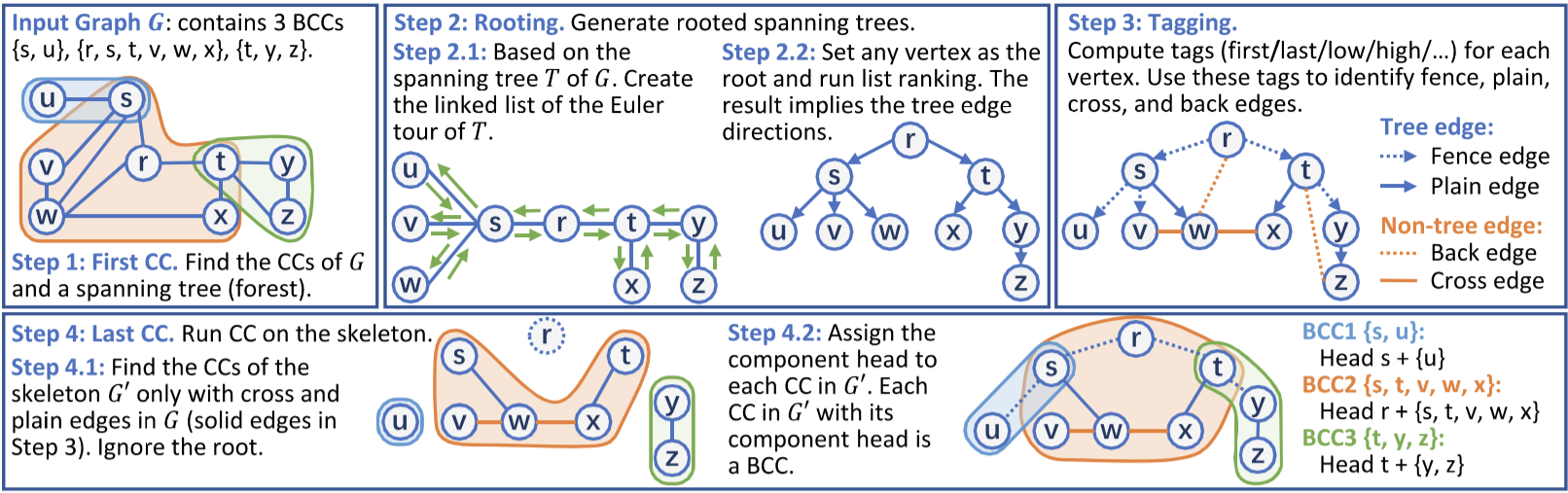
- 将双连通图(BCC)的并行转化为两次连通图(CC)的并行。
- 证明了算法的正确性。
- 对算法进行了实现,在多种workload下均有较好的表现。
评价
- 算法流程简明,实现高效,非常不错的论文。
- 对于图的生成树以及相关处理方式值得学习。
总结
双连通分量(BCC)的求解是图论中的基础问题,可以广泛应用于如平面性检验、中心性计算和网络分析等任务中。Hopcroft-Tarjan算法是串行求解BCC的经典算法,其时间复杂度




双连通分量(BCC)的求解是图论中的基础问题,可以广泛应用于如平面性检验、中心性计算和网络分析等任务中。Hopcroft-Tarjan算法是串行求解BCC的经典算法,其时间复杂度