Learning Rate Based Branching Heuristic for SAT Solvers

简介

分支启发：决策变量的选择

现有分支启发方法：

• VSIDS(2001)及其变体：最有效、最主要
  • Glucose、Lingeling、CryptoMiniSat
• 基于冲突历史(Conflict History-Based, CHB)的分支启发：作者提出，效果优于VSIDS
• 学习率分支(Learing Rate Branching, LRB)：本文介绍，将分支启发转化为优化问题，效果优于VSIDS和CHB

学习率

想法：决策变量要尽可能多的参与到子句学习的过程中

定义：，其中代表被决策赋值到被取消赋值的过程中产生的学习子句，代表参与生成的子句数量，代表总子句数量。

假设以下过程：

• Iter 100：被选为决策变量
• Iter 101&104：参与了冲突分析过程，生成了学习子句
• Iter 105：由于非时间顺序的回溯，被取消赋值

该过程中

多臂赌博机(Multi-Armed Bandit, MAB)

• 经典场景：赌博机有n个拉杆，拉杆的奖励分布是隐藏的，目标为多次拉动最大化总收益

  • 探索：尝试不同的拉杆以了解奖励分布
  • 利用：根据以往的经验，选择目前期望收益最高的拉杆

• 学习率优化：SAT问题有n个变量，每个变量的学习率是隐藏的，目标为选择尽可能少的决策变量，生成尽可能多的子句

  • 探索：尝试不同的决策变量，得到实际学习率作为奖励
  • 利用：根据以往的经验，选择目前学习率最高的未被赋值的变量

具体实现

• 指数移动平均更新学习率：​
  • 使用优先队列储存学习率，的更新与选择
• 步长逐步减小：
• 原因侧补偿：，其中代表在决策路径上但不在First UIP后的学习子句数量
• 提升局部性：每次冲突分析后

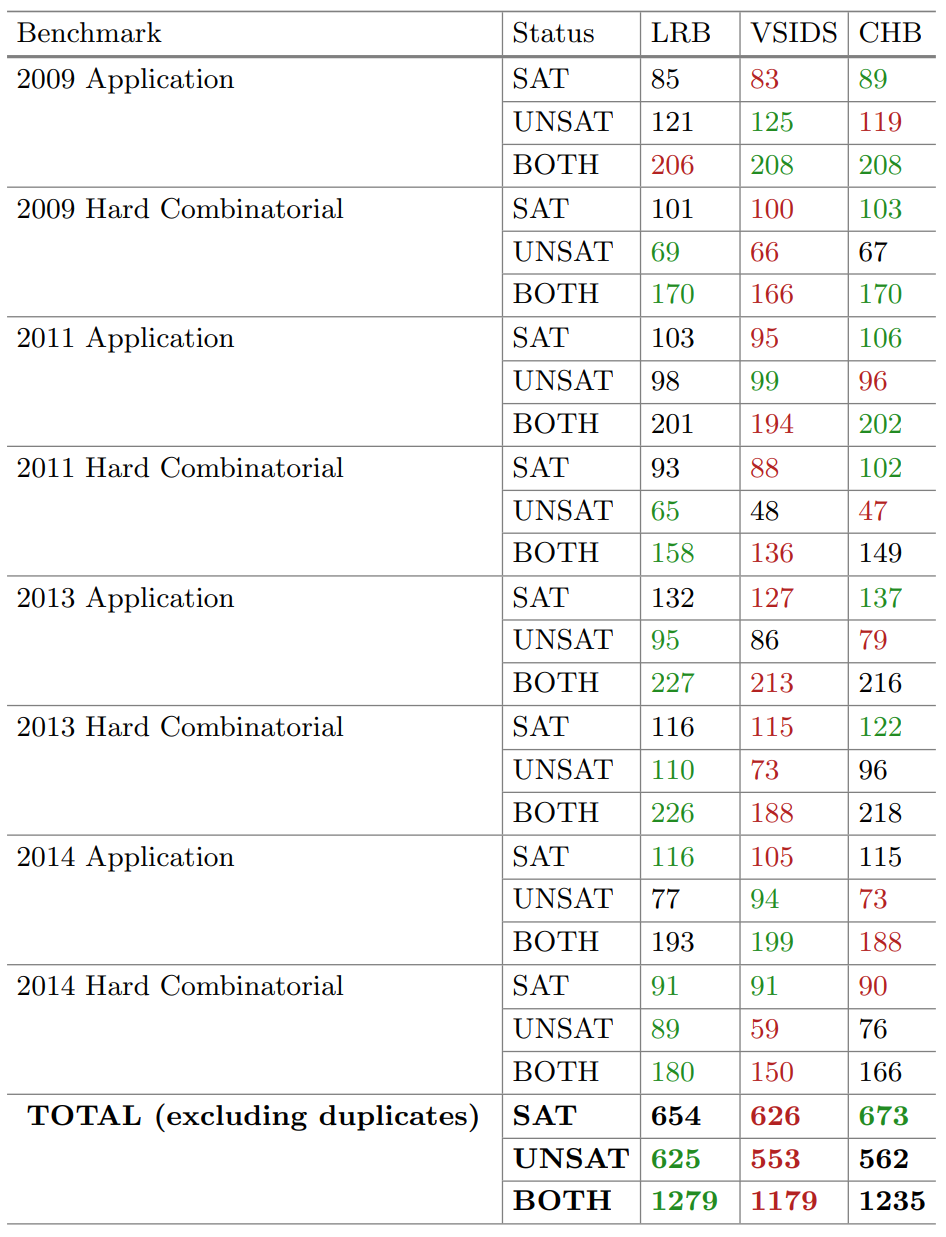
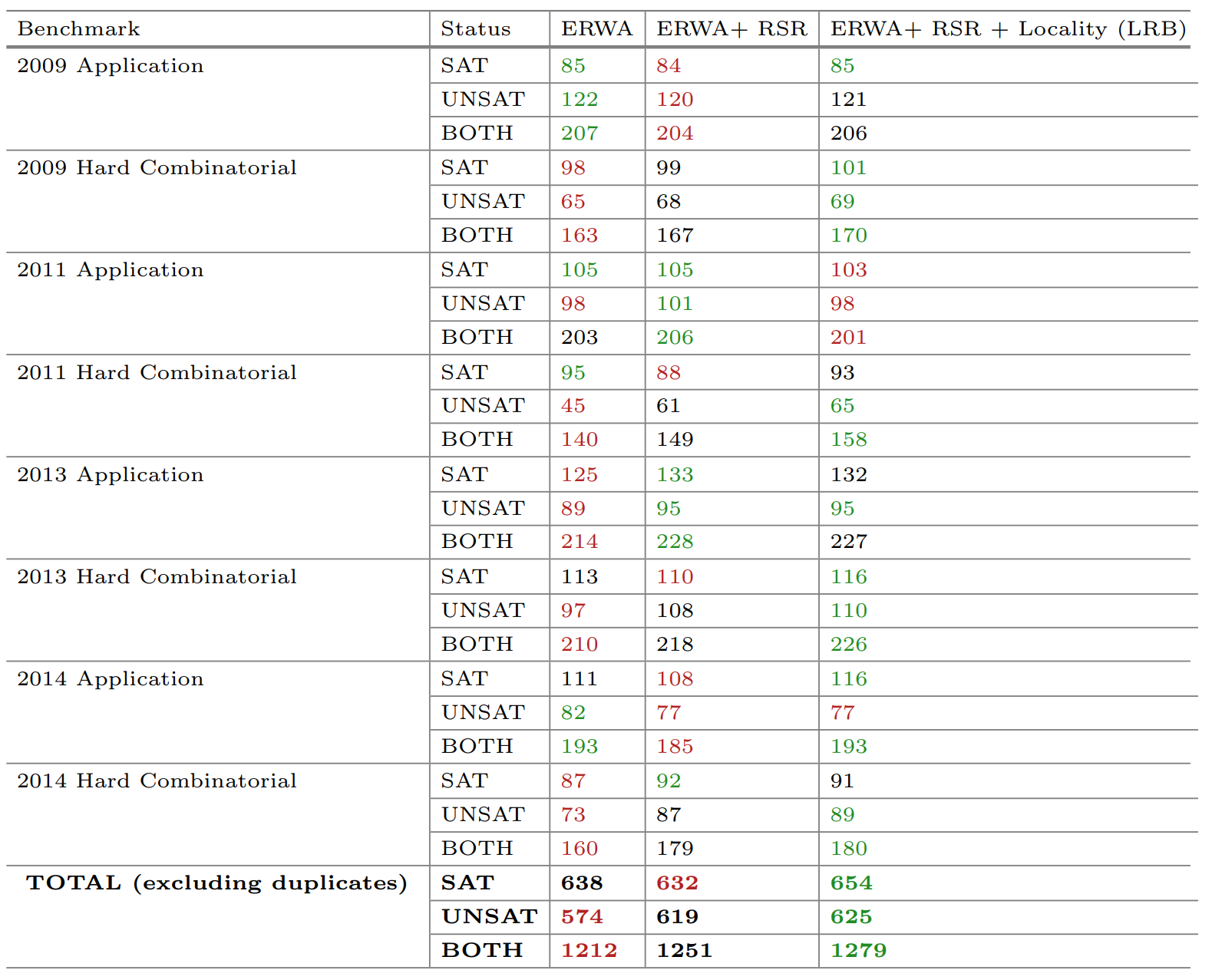
评价

• 学习率指标的想法、制定和计算的开销都很合理
• 事实：以传统的多臂赌博机视角来看，最终的实现只有利用（每次选择当前的最优值）；但以SAT问题来看，多次利用可以起到探索的作用

总结

SAT问题是一个经典的NP完全问题。许多其他领域的问题都可以转化为SAT问题，并利用SAT求解器进行求解。分支启发是现代SAT求解器的关键部分之一。一个优秀的分支启发算法可以加速学习子句的生成，提高现代SAT求解器的效率。分支启发关注的问题是搜索过程中如何选择下一个进行赋值的变量。作者将该问题类比于强化学习领域的多臂赌博机问题，将变量赋值期间对生成学习子句的贡献率类比于多臂赌博机的收益。作者使用指数移动平均计算期望收益，同时结合步长和权重衰减技巧提高搜索的局部性，加入原因侧补偿项提高收益的完整性，最终提出学习率分支(LRB)启发算法。该算法相较于被广泛应用的经典分支启发算法VSIDS，具有显著的性能提升，而且计算开销较小，可以应用于后续的SAT求解器。(300)