核心想法
-
Kannan算法:先将格基预处理为准HKZ基(缺陷:速度慢),再进行枚举算法
-
预处理和枚举都是递归的过程
- 删除单次递归中不必要的运算
- 增加递归的步长
实验结果
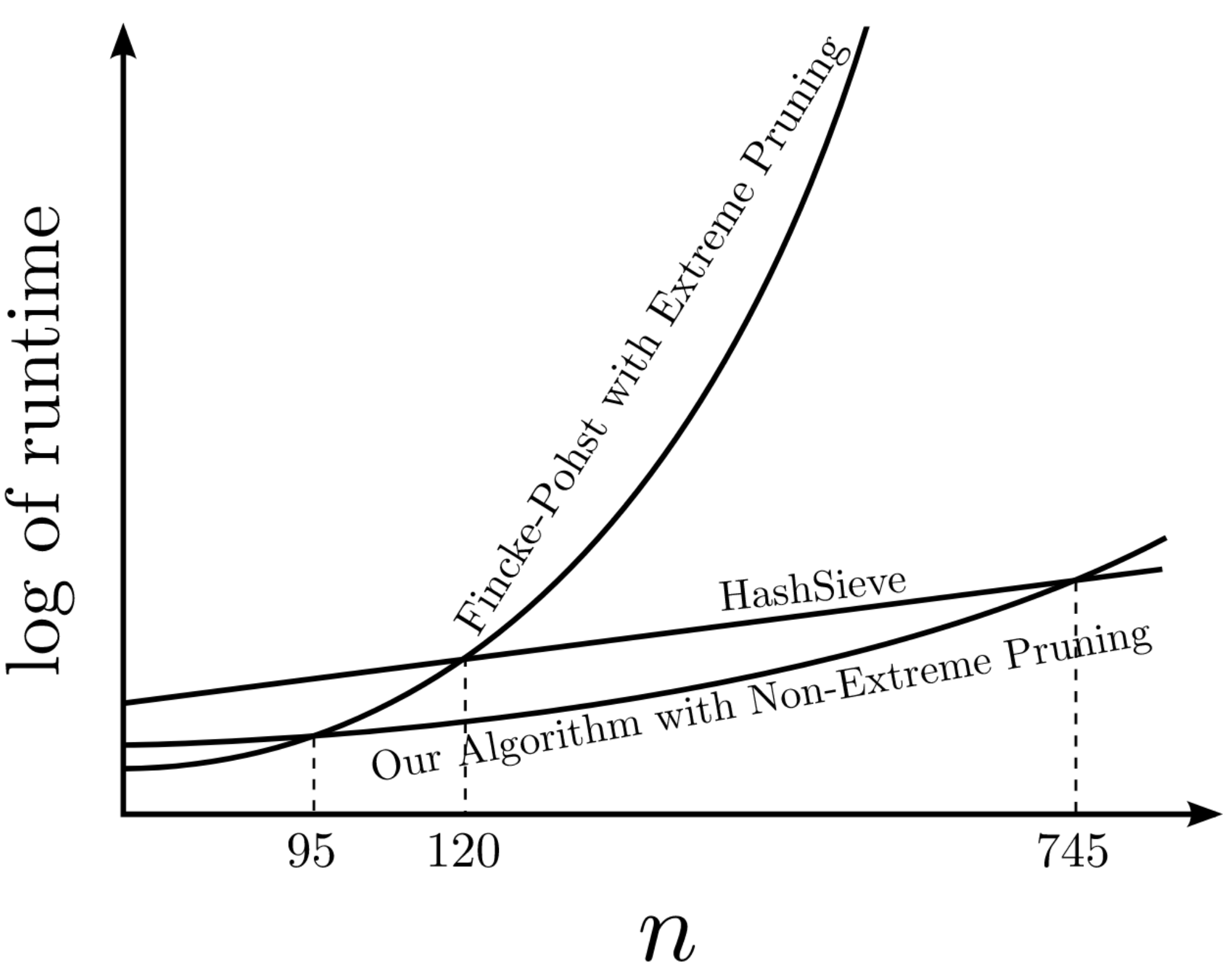
论文贡献
-
提出并实现了预处理代价更小的,时间复杂度为
-
提出并实现了存在线性相关性的投影格上的枚举方法
-
SVP求解速度优于现有的枚举算法
个人评价
-
增加递归的步长,虽然在时间复杂度上没有区别,但在实际表现中有性能提升
-
重新思考SubSieve,在投影格上进行筛法并提升的核心想法其实是来源于枚举算法
改进思路:
-
与BKZ算法进行结合
-
剪枝
总结
格中最短向量问题(SVP)是格密码学中的核心难题。格密码中许多底层问题(NTRU,SIS,LWE)的密码学分析都可以归结为格中最短向量问题。SVP求解算法分为两类:枚举与筛选。枚举算法使用递归投影进行遍历;筛选算法对大规模的向量集合进行内部组合,逐步降低向量集合的整体长度。Kannan提出的理论枚举算法虽然具有较低的时间复杂度,但由于预处理过程过于耗时,没有被用于实际求解。作者对Kannan的算法进行了分析,采用了简化预处理过程,增加递归步长等多种方法,实现了时间复杂度较低且实际可行的枚举算法,表现优于现有的枚举算法和筛法。我认为论文中算法提升效率的核心是增加递归步长,虽然没有改进理论时间复杂度,但提升了实际求解效率,后续可以尝试使用BKZ算法以及剪枝进一步提升枚举算法的效率。(305)