LAB-PQ实现
-
基于锦标赛树的LAB-PQ实现
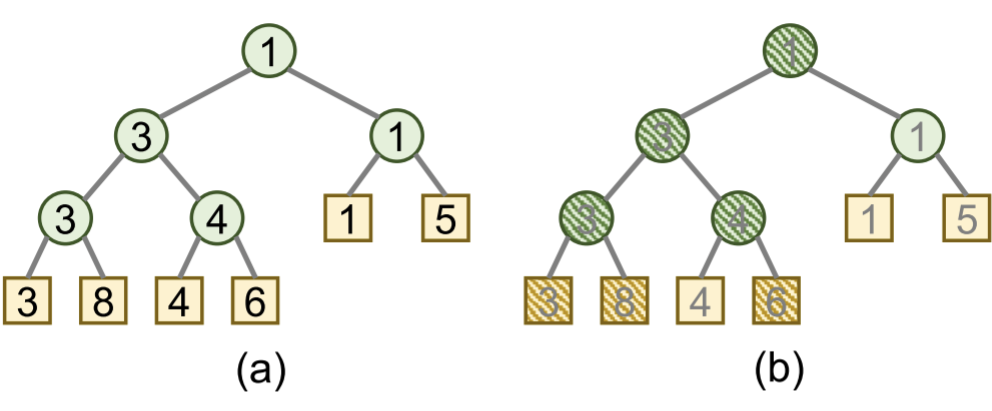
基于树存储的LAB-PQ,展示原理
def _mark(id, newflag):
t = T.leaf(id)
t.inQ = newflag
while t != T.root and
TestAndSet(t.parent.renew, newflag) :
t = t.parent
def _sync(t):
if t.is_leaf() :
return Q[t.id] if t.inQ else +inf
if t.renew == 0 :
return t.k
t.renew = 0
leftKey, rightKey = _sync(t.left),
_sync(t.right) #parallel
t.k = min(leftKey, rightKey)
return t.k
def _extract_from(theta, t):
if t.is_leaf() :
if Q[t.id] <= theta :
mark(t.id, 0)
return [t.id]
return []
if t.k > theta :
return []
leftSeq, rightSeq = _extractfrom(theta, t.left),
_extract_from(theta, t.right) #parallel
return leftSeq + rightSeq
def update(id):
_mark(id, 1)
def extract(theta):
_sync(T.root)
return _extract_from(theta, T.root)
具体实现时采用树状数组。
实现细节优化
- 稀疏-密集优化:在邻居较少时,使用数组存储id;在邻居较多时,使用位标识与每个邻居是否有边。
- 无向图的优化:算法框架第10行,优先使用v的邻居进行松弛。
- 𝜌-Stepping中𝜌的选择:部分采样排序,按比例选择阈值
- 邻居较多时的优化:邻居较多时可能导致同步更新负担过大,提前进行同步更新。
评价
- 主要贡献:LAB-PQ的提出与无锁的实现。
- 次要贡献:对现有的并行SSSP算法进行了框架梳理,并提出了新的超参数不敏感的SSSP算法。
- 个人思考:先对需要实现的功能进行抽象,再进行数据结构或算法的设计。